Задачи на логику. Часть 25
Большой сборник задач на логику с ответами (двадцать пятая часть). Умение решать логические задачи формирует мышление и развивает логику человека.
Сборник логических задач с ответами. Часть 25
Юный сторож

Торговец привез на рынок мешки с орехами, скинул с телеги, отправил лошадь назад – и вдруг вспомнил, что ему необходимо отлучиться и притом надолго. Оставить товар без призора нельзя, надо кому нибудь поручить сторожить, – но кому? «Как бы это устроить подешевле?» – размышлял торговец.
В это время взгляд его упал на мальчика Степку, беспризорного, который ежедневно являлся на рынок в поисках какой нибудь работы: то тачку перевезет, то поможет овощи раскладывать, то место расчистить – вот и сыт на день. Степка был честный и шустрый мальчик; работу давали ему охотно.
– Степка, постереги орехи, – обратился к нему наш торговец.
– Надолго?
– Не знаю, как придется. А тебе что: я заплачу.
– Сколько же заплатите?
– А сколько тебе хочется? – осторожно осведомился торговец, боясь переплатить.
Степка подумал и сказал:
– За первый час дайте один орех.
– Идет. За второй?
– Два.
– Согласен. А если придется и третий час сторожить?
– Тогда прибавите четыре ореха. Коли и тогда не вернетесь, то за четвертый час уплатите восемь орехов; за пятый – шестнадцать, за шестой…
– Ладно, – перебил его торговец, – нечего долго болтать: за каждый следующий час вдвое против предыдущего. Согласен. Только не смей с места уходить: стереги, хотя бы я и до ночи не возвратился.
Торговец ушел, довольный тем, что отыскал дешевого сторожа: за горсть орехов будет хоть целые сутки сторожить.
Справил торговец свое дело только к вечеру. Надо бы на рынок возвратиться, но торговец наш не торопится. «Ночью какая торговля? Товар под надзором, сторож никуда не уйдет. Отсыплю ему еще пригоршню орехов», – подумал торговец и завалился спать.
Тем временем Степка честно сторожил мешки с орехами и нисколько не горевал, что хозяин не является. Наступила ночь, все стали с рынка расходиться, но Степка крепко держал уговор: разлегся у мешков и чему-то ухмыляется.
Когда на другое утро торговец явился к своим мешкам, он застал Степку накладывающим его орехи на тачку.
– Стой! Ты куда, злодей, собираешься мой товар увозить?
– Был ваш, теперь мой, – спокойно ответил Степка. – Забыли, что ли, уговор?
– Уговор! Да ведь по уговору ты сторожить обязан, а ты воровать хочешь.
– Свое увожу, не краденое. Это мне следует за то, что я сутки сторожил.
– Сутки сторожил, так тебе весь товар отдавай? Бери, сколько следует, а моего трогать не смей…
– Я и беру, что следует. Не только лишнего не беру, мне еще с вас причитается.
– С меня следует? Вот это хорошо! Сколько же тебе прибавить надо?
– Да примерно в тысячу раз больше, чем тут у вас имеется. Тогда, пожалуй, в расчете будем.
– За одни то сутки? Да ты, брат, совсем считать не умеешь!
А как вы думаете: кто из них двоих не умел считать?
В это время взгляд его упал на мальчика Степку, беспризорного, который ежедневно являлся на рынок в поисках какой нибудь работы: то тачку перевезет, то поможет овощи раскладывать, то место расчистить – вот и сыт на день. Степка был честный и шустрый мальчик; работу давали ему охотно.
– Степка, постереги орехи, – обратился к нему наш торговец.
– Надолго?
– Не знаю, как придется. А тебе что: я заплачу.
– Сколько же заплатите?
– А сколько тебе хочется? – осторожно осведомился торговец, боясь переплатить.
Степка подумал и сказал:
– За первый час дайте один орех.
– Идет. За второй?
– Два.
– Согласен. А если придется и третий час сторожить?
– Тогда прибавите четыре ореха. Коли и тогда не вернетесь, то за четвертый час уплатите восемь орехов; за пятый – шестнадцать, за шестой…
– Ладно, – перебил его торговец, – нечего долго болтать: за каждый следующий час вдвое против предыдущего. Согласен. Только не смей с места уходить: стереги, хотя бы я и до ночи не возвратился.
Торговец ушел, довольный тем, что отыскал дешевого сторожа: за горсть орехов будет хоть целые сутки сторожить.
Справил торговец свое дело только к вечеру. Надо бы на рынок возвратиться, но торговец наш не торопится. «Ночью какая торговля? Товар под надзором, сторож никуда не уйдет. Отсыплю ему еще пригоршню орехов», – подумал торговец и завалился спать.
Тем временем Степка честно сторожил мешки с орехами и нисколько не горевал, что хозяин не является. Наступила ночь, все стали с рынка расходиться, но Степка крепко держал уговор: разлегся у мешков и чему-то ухмыляется.
Когда на другое утро торговец явился к своим мешкам, он застал Степку накладывающим его орехи на тачку.
– Стой! Ты куда, злодей, собираешься мой товар увозить?
– Был ваш, теперь мой, – спокойно ответил Степка. – Забыли, что ли, уговор?
– Уговор! Да ведь по уговору ты сторожить обязан, а ты воровать хочешь.
– Свое увожу, не краденое. Это мне следует за то, что я сутки сторожил.
– Сутки сторожил, так тебе весь товар отдавай? Бери, сколько следует, а моего трогать не смей…
– Я и беру, что следует. Не только лишнего не беру, мне еще с вас причитается.
– С меня следует? Вот это хорошо! Сколько же тебе прибавить надо?
– Да примерно в тысячу раз больше, чем тут у вас имеется. Тогда, пожалуй, в расчете будем.
– За одни то сутки? Да ты, брат, совсем считать не умеешь!
А как вы думаете: кто из них двоих не умел считать?
В зеркале

Который год XIX столетия увеличивается в 41/2 раза, если на него смотреть в зеркало?
Какие числа?

Какие два целых числа, если их перемножить, составят семь?
Не забудьте, что оба числа должны быть целые, поэтому такие ответы, как З1/2 × 2 или 21/3 × 3, не подходят.
Не забудьте, что оба числа должны быть целые, поэтому такие ответы, как З1/2 × 2 или 21/3 × 3, не подходят.
Сложить и перемножить

Какие два целых числа, если их сложить, дают больше, чем если их перемножить?
Три числа

Какие три целых числа, если их перемножить, дают столько же, сколько получается от их сложения?
Столько же

Какие два целых числа, если их перемножить, дают столько же, сколько получается от их сложения?
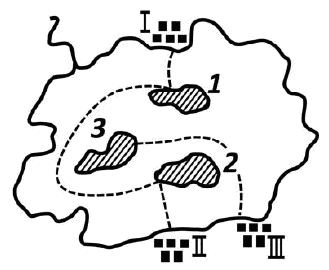
Три острова

На озере три острова, которые отмечены на нашем чертеже цифрами 1, 2 и 3. А на берегу расположено три рыбачьих поселка: I, II и III.
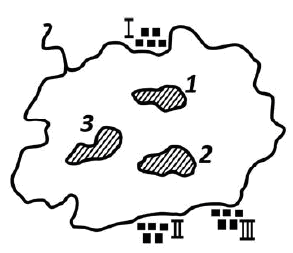
Лодка отплывает из поселка I, посещает острова 1 и 2 и пристает к поселку II.
Одновременно из поселка III отплывает другая лодка, пристающая к острову 3. Пути обеих лодок не пересекаются.
Можете ли вы начертить эти пути?

Лодка отплывает из поселка I, посещает острова 1 и 2 и пристает к поселку II.
Одновременно из поселка III отплывает другая лодка, пристающая к острову 3. Пути обеих лодок не пересекаются.
Можете ли вы начертить эти пути?
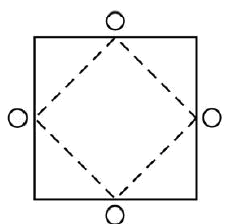
Деревьев не рубить

На этом чертеже квадрат обозначает пруд, а четыре кружочка близ углов – деревья. Надо расширить пруд до размера, вдвое большего по площади, но так, чтобы деревья не срубать.
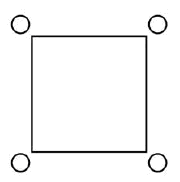
Возможно ли это сделать?

Возможно ли это сделать?
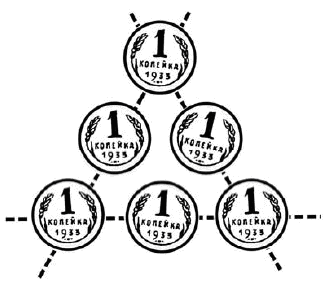
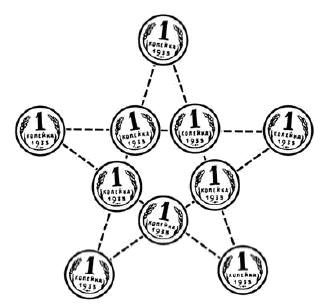
Шесть копеек

Надо разложить шесть копеечных монет в три прямых ряда так, чтобы в каждом ряду было по три копейки.
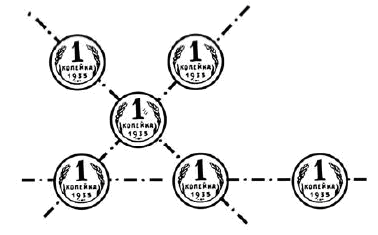
Вы думаете – это невозможно? Не хватает еще трех монет? А вот поглядите, они здесь расположены на рисунке.
Вы видите здесь три ряда монет, по три в каждом ряду. Значит, задача решена. Правда, ряды перекрещиваются, но ведь не запрещено было их перекрещивать.
Теперь попробуйте сами догадаться, как можно решить ту же задачу еще и другим способом.

Вы думаете – это невозможно? Не хватает еще трех монет? А вот поглядите, они здесь расположены на рисунке.
Вы видите здесь три ряда монет, по три в каждом ряду. Значит, задача решена. Правда, ряды перекрещиваются, но ведь не запрещено было их перекрещивать.
Теперь попробуйте сами догадаться, как можно решить ту же задачу еще и другим способом.
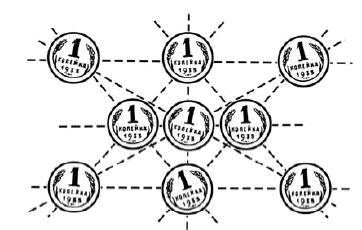
Девять монет

Надо расположить девять монет в десять рядов по три монеты в каждом ряду. Можно ли это сделать?
В пять рядов

Десять монет надо расположить в пять прямых рядов так, чтобы в каждом ряду лежало по четыре монеты.
Прибавлю, что ряды могут перекрещиваться.
Прибавлю, что ряды могут перекрещиваться.
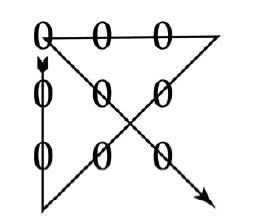
Девять нулей

Девять нулей расставлено так, как показано на рисунке:
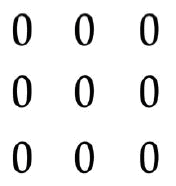
Задача состоит в том, чтобы перечеркнуть все нули, проведя только четыре прямых линии.
Можете ли вы это сделать?
Чтобы облегчить вам отыскание решения, прибавлю еще, что все девять нулей перечеркиваются при этом одним росчерком (т. е. не отрывая пера от бумаги).
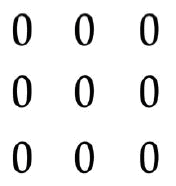
Задача состоит в том, чтобы перечеркнуть все нули, проведя только четыре прямых линии.
Можете ли вы это сделать?
Чтобы облегчить вам отыскание решения, прибавлю еще, что все девять нулей перечеркиваются при этом одним росчерком (т. е. не отрывая пера от бумаги).
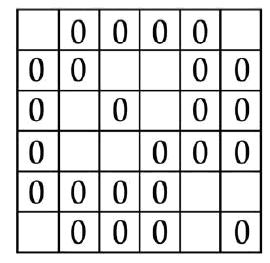
Тридцать шесть нулей

В клетках этой решетки расставлено, как видите, 36 нулей.
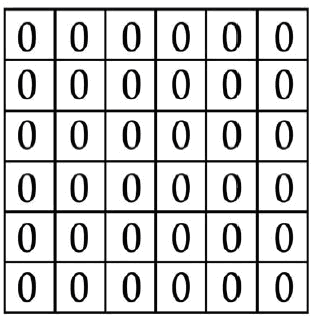
Двенадцать из них надо зачеркнуть, но так, чтобы после этого в каждом вертикальном и горизонтальном ряду оставалось по одинаковому количеству незачеркнутых нулей.
Какие же нули надо зачеркнуть?

Двенадцать из них надо зачеркнуть, но так, чтобы после этого в каждом вертикальном и горизонтальном ряду оставалось по одинаковому количеству незачеркнутых нулей.
Какие же нули надо зачеркнуть?
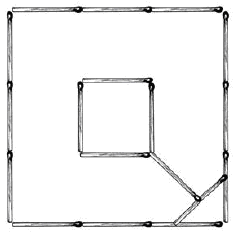
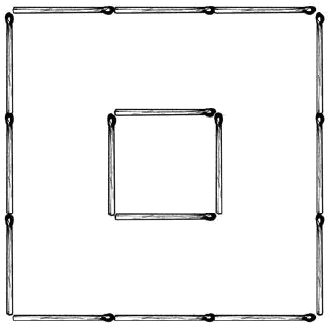
Мостик

Сложите из спичек два квадрата один в другом, как показано на рисунке. Внутренний маленький квадрат пусть изображает островок, окруженный канавой. Через эту канаву нужно перекинуть мостик из двух спичек. Как устроить такой мост, обойдясь только двумя спичками?

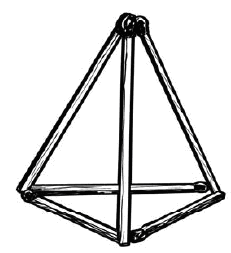
Из шести спичек

Из шести спичек составить четыре равносторонних треугольника.
Само собою разумеется, что переламывать спички нельзя.
Задача интересна тем, что с первого взгляда кажется совершенно неразрешимой.
Само собою разумеется, что переламывать спички нельзя.
Задача интересна тем, что с первого взгляда кажется совершенно неразрешимой.
Похожие материалы: